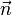矩陣運算
矩陣相加 對應元素相加
矩陣相減 對應元素相減
矩陣相乘 每個元素就是兩個矩陣的行與列點積。所以兩個矩陣的行與列維度要相同。
矩陣數乘 每個元素乘上一個數
矩陣相等 對應的每個元素相等
矩陣相乘
條件
假設A矩陣*B矩陣
則A行向量的元素個數=B列向量元素個數
(大陸橫為行,直為列)
否則無法相乘
A=[1- 5 -4]
[3 2 1]
B=[2 1 0 ]
[0 -2 1]
[-1 2 3]
AB=[(-1,5,-4).(2,0,-1) (-1,5,-4).(1,-2,2) (-1,5,-4).(0,1,3)]
[(3,2,1).(2,0,1) (3,2,1).(1,-1,2) (3,2,1)(0,1,3)]
行.列 (點積)
矩陣乘法不滿足交換率
A*B != B*A
矩陣乘法滿足結合率
A(B+C)=AB+AB
(AB)C=A(BC)
矩陣除法
矩陣運算沒有除法
向量矩陣
行向量矩陣
A=[1 3 3]
列向量矩陣
B= [2]
[2]
[3]
向量-矩陣乘法
OpenGL 左乘方式--矩陣在左,向量在右 記憶法(
O在左)
DirectX 右乘方式--矩陣在右,向量在左 記憶法
(X在右)
因為矩陣乘法不反足交換率,所以在左在右結果不同。
轉置矩陣(Transpose)
把一個矩陣的行和列互換。mxn的轉置矩陣就是nxm。
原矩陣的行向量=轉置矩陣的列向量
A=[1 1 1 ]
[2 2 2]
C=A.transpose
[1 2]
[1 2]
[1 2]
B=[a b c d]
D=B.transpose
[a]
[b]
[c]
[d]
A*B=(D*C).transpose
範例
A,B兩向量
C=A.transpose
D=B.transpose
A*B ↘︎ C*D => A*B=D*C 兩個剛好交錯
B*A ↗︎ D*C => B*A=C*D
矩陣乘以向量
1 矩陣維度與向量元素個數不需相同
2 矩陣*向量 =>變成向量
3 矩陣*向量=向量*矩陣轉置(要自己計算)
向量 X=(1,2,3,4);
A=[1 1 1 1]
[2 2 2 2]
[3 3 3 3]
[4 4 4 4]
A*X=(1111.(1234) 2222.(1234) 3333.(1234) 4444.(1234))
A.transpose=
[1 2 3 4]
[1 2 3 4]
[1 2 3 4]
[1 2 3 4]
X*A.transpose
((1234)(1111) (1234)(2222) (1234)(3333) (1234)(4444))
Unity中矩陣乘以向量
可以直接矩陣*向量
不能向量*矩陣 (要自己計算)
矩陣A
向量V
A*V =>ok
V*A =>error
單位矩陣
1 是正方形矩陣
2 中心左上右下斜對角線(back slash)的元素都是1
3 其他元素都是0
4 任何矩陣*單位矩陣,結果不變
5 單位矩陣就是矩陣中的數字1(跟單位向量相同)
[1 0 0]
[0 1 0]
[0 0 1]
逆矩陣(Inverse)
1 矩陣運算沒有除法
2 只有
正方形矩陣才能夠逆運算
3 一個nxn的矩陣的逆矩陣,仍然是nxn的矩陣
4 不是所有的矩陣都有逆矩陣,有逆矩陣的矩陣稱為可逆
5 如果有可逆矩陣,這個逆矩陣一定是唯一的
6 將一個矩陣與他的逆矩陣相乘,結果一定為單位矩陣
有矩陣A,B,C,且A=B*C,且D為C的逆矩陣
A=BC
AD=BDC (DC=1)
AD=B
範例
有一點a
一矩陣b
d=b的逆矩陣
轉換後的點c = a*b
cd=a*b*d (bd=1)
cd=a
可找到原始的a點
常用來把點從局部空間轉換到世界空間,
或從世界空間轉換回局部空間。
矩陣計算平移
1 點的位移向量,使用DirectX要寫在矩陣第四行的前三個,
因為如果寫在前三行,那會被x,y,z乘到
只能寫在第四行的前三個,經過計算後就分別被x,y,z加
使用OpenGL則分別寫在前三行的最後一元素
directX與openGL可使用矩陣轉置來切換
2 矩陣的每個位置數字都有意義,都是經過設計的
3 因為3x3不夠用,所以擴充為4x4,自己新增w
4 當w=0,(x,y,z,0) 就是用來描述向量 =>可得到原始向量
5 當w=1,(x,y,z,1) 就是用來描述點 =>可算出位移後的點
DirectX計算(右乘,矩陣在右,向量在左)
A=[x,y,z,w] 行向量
M= 單位矩陣
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
A*M=
x*1+y*0+z*0+w*0=x
x*0+y*1+z*0+w*0=y
x*0+y*0+z*1+w*0=z
x*0+y*0+z*0+w*1=w
假設位移向量B=(tx,ty,tz),則A位移後的點為(x+tx,y+ty,z+tz)
tx,ty,tz寫在矩陣最下行靠左
m=
1 0 0 0
0 1 0 0
0 0 1 0
tx ty tz 1
A*m=[x,y,z,w] *m=
x*1+y*0+z*0+w*tx=x+wtx
x*0+y*1+z*0+w*ty=y+wty
x*0+y*0+z*1+w*tz=z+wtz
x*0+y*0+z*0+w*1=w
當w=1,結果就是 x+tx,y+ty,z+tz,1
因為w是我們自己擴充的,所以可設為1
所以經由以上算法,點A的位移,利用矩陣運算可得到結果。
矩陣每個位置的數字都有固定意義,都事先設定好的。
OpenGL計算(左乘,矩陣在左,向量在右 =Unity的系統 )
A=[x,y,z,w] 行向量
M= 單位矩陣
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
M*A=
x*1+y*0+z*0+w*0=x
x*0+y*1+z*0+w*0=y
x*0+y*0+z*1+w*0=z
x*0+y*0+z*0+w*1=w
假設位移向量B=(tx,ty,tz),則A位移後的點為(x+tx,y+ty,z+tz)
tx,ty,tz寫在矩陣前三行最末位
m=
1 0 0 tx
0 1 0 ty
0 0 1 tz
0 0 0 1
m*A=m*[x,y,z,w] =
1*x+0*y+0*z+w*tx=x+wtx
0*x+1*y+0*z+w*ty=y+wty
0*x+0*y+1*z+w*tz=z+wtz
0*x+0*y+0*z+w*1=w
當w=1,結果就是 x+tx,y+ty,z+tz,1
因為w是我們自己擴充的,所以可設為1
矩陣計算縮放
1 縮放就是倍數的關係,所以(x,y,z)要能分別乘以縮放的數字
2 因此只能放在斜對角線的元素位置上
sx 0 0 0
0 sy 0 0
0 0 sz 0
0 0 0 0
假設x放大2,y所小0.5,z放大3,那就是
2 0 0 0
0 0.5 0 0
0 0 3 0
0 0 0 0
範例
矩陣A=
[1 0 0 0]
[0 2 0 0]
[0 0 0.5 0]
[0 0 0 1]
向量V=[x,y,z,w]
v*A=
x*1+y*0+z*0+w*0=x
x*0+y*2+z*0+w*0=2y
x*0+y*0+z*0.5+w*0=0.5z
x*0+y*0+z*0+w*0=w
=[x,2y,0.5z,0]
=x不變,y放大2,z縮小0.5
矩陣計算旋轉
1 旋轉要考慮軸
2 旋轉要考率角度(非弧度)
假設延n軸旋轉 n=(x,y,z)
轉 a角度
c=cos(a)
s=sin(a)
矩陣為:
c+(1-c)*x*x (1-c)*x*y+s*z (1-c)*x*z-s*y 0
(1-c)*x*y-s*z c+(1-c)*y*y (1-c)*y*z+s*x 0
(1-c)*x*z+s*y (1-c)*y*z-s*x c+(1-c)*z*z 0
0 0 0 1
範例
假設延x軸旋轉 (1,0,0)
1 0 0 0
0 cos(a) sin(a) 0
0 -sin(a) cos(a) 0
0 0 0 1
矩陣組合
1 如果一次要計算三個矩陣(平移矩陣,縮放矩陣,旋轉矩陣),太消耗資源
2 利用矩陣乘法分配律,可以把三個矩陣先相乘,在跟向量相乘,可以少算2/3次
3 同時三個矩陣組成一個,也方便處理
4 組合方式是三個矩陣相乘