向量

向量的意義

向量是同時具有大小和方向的物理量

勢能：在某方向上施加一定的作用力

位移：在某方向上移動的一度距離

速度：速率和方向

用來表示方向

遊戲中角色方向

多邊形面對的方向

光線的方向

反射光的方向

向量幾何意義

兩個向量可以：
確定一個三角形
確定一個平行四邊形
確定一個平面

向量運算

向量相加  對應的元素相加
向量相減  對應的元素相減
向量數乘  每個元素乘上一個數
向量叉積  就是第三個同時垂直原向量的向量。不含自己，前減後，↘︎↙︎↘︎ 。|A||B|Sin(a)
向量點積  對應元素相乘，加起來。變成一個數。|A||B|Cos(a)
向量相等  方向相同，大小相等就是兩個相等向量

向量計算

向量計算一定是把向量頭部移到原點

也就是假設向量從原點出發

向量加法

定義

兩個同維度(2D和2D或3D和3D)的向量相加，
就是兩個向量的對應分量相加。
x+x
y+y
z+z

u=(ux,uy,uz)
v=(vx,vy,vz)
u+v=(ux+vx,uy+vy,uz+vz)

幾何意義

A=(xa,yz)
B=(xb,yb)
C=(xc,yc)

AB=(xb-xa,yb-ya)
BC=(xc-xb,yc-yb)
AC=(xc-xa,yc-ya)

AB+BC=(xb-xa+xc-xb,yb-ya+yc-yb)=(xc-xa,yc-ya)=AC
頭尾相連的兩個向量相加，結果從頭到尾的那個向量

AC就是平行四邊形的對角線
是兩向量行成的夾角內的對角線
因此兩個向量相加可以確定一個平行四邊形

AC也是兩向量頭尾相連的三角形的第三邊
所以可以求第三邊的長度及方向

平行四邊形面積= 底*高
所以向量可以算出平行四邊形面積

三角形面積=平行四邊形面積/2


結論

向量加法就是：兩項量移動成頭尾相連，所形成的第三邊。

因為向量有相等性，可以平移，
所以任何兩個向量，一定可以平移成頭尾相連。

向量減法

定義

兩個同維度(2D和2D或3D和3D)的向量相減，
就是兩個向量的對應分量相減。
x-x
y-y
z-z

u=(ux,uy,uz)
v=(vx,vy,vz)
u-v=(ux-vx,uy-vy,uz-vz)

幾何意義

AB=(xb-xa,yb-ya)
AC=(xc-xa,yc-ya)
BC=(xc-xb,yc-yb)


AB-AC=(xb-xa-xc+xa,yb-ya-yc+ya)=(xb-xc,yb-yc)=CB

CB是兩向量形成的平行四邊形的對角線(非兩向量形成的夾角內的對角線)
所以也可確定一個平行四邊形

CB是兩向量尾部相連形成的三角形的第三邊
CB可以求第三邊的長度及方向

結論

向量減法就是：兩向量移動成起點相連形成的第三邊
方向指向被減向量。(減號前方的是被減數)

向量減法就是向量加法加上負向量，
所以用向量加法來思考即可。

向量叉積 

向量叉積 Cross Product
向量外積 Outer Product
向量積Vector Product

A,B兩向量叉積(A X B) 會得到一個垂直於這兩個向量的第三個向量
B,A兩向量叉積(B X A) 會得到一個垂直於這兩個向量的第三個向量，但與A X B 方向相反

A ∧ B = - A ∧ B 
各自算出的結果是兩個方向相反，大小相同向量
就是反交換律

寫作

×（有時也被寫成∧，避免和字母x混淆）

公式

A X B =|A||B|Sin𝛳
θ表示和之間的角度（0°≤θ≤180°），它位於這兩個矢量所定義的平面上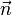
是一個與、所構成的平面垂直的單位矢量。
https://zh.wikipedia.org/wiki/%E5%90%91%E9%87%8F%E7%A7%AF

直接算法

A=(ax,ay,az)
B=(bx,by,bz)

A x B=(ay*bz - az*by) =x          記憶法 ↘︎  不含自己    前減後
            (az*bx - ax*bz) =y                       ↙︎
            (ax*by - ay*bx) =z                      ↘︎

幾何意義

叉積可得到垂直於AB平面的法向量。

向量點積

向量點積 Dot Product
向量內積 Inner Product
標向量 Scalar Product

 兩向量計算點積會得到一個純量，不帶方向只有大小

寫作

. 

公式

A.B=|A||B|cos𝛳

𝛳是AB間的最小夾角。即0<= 𝛳<=180
兩個向量必須共起點
當A,B都是單位向量時，A.B=1*1*cos𝛳=cos𝛳 , => -1<=cos𝛳<=1
cos𝛳一定大於等於-1，小於等於1

直接算法

A=(ax,ay,az)
B= (bx,by,bz)

A.B =ax*bx+ay*by+az*bz  =>只有大小  記憶法：分量相乘，加起來

AB都是單位向量，可推斷出角度

就可直接得到cos𝛳的值
若cos𝛳的值是已知的，那就可以知道角度是多少
ABcos𝛳=0.95 ，𝛳=18
因為cos(18)=0.95

幾何意義

無，但有一些性質

利用cos𝛳可得到一些性質
cos𝛳 0度=1
cos𝛳 90度=0
cos𝛳 180度=-1

所以 A.B=0  =>cos𝛳=0  => 𝛳 =90度 => A,B垂直
所以 A.B>0  =>cos𝛳>0  => 𝛳 <90度 =>A,B夾角小於90度
所以 A.B<0  =>cos𝛳<0  => 𝛳 >90度 =>A,B夾角大於90度

平面法線跟光的角度越小，光越強
平面法線跟光的角度越大，光越弱
正好符合cos，所以可以用cos(𝛳)來計算光的強弱
光最後的顏色=光的顏色*cos(𝛳)

向量大小(長度)

向量長度符號
||U||=√a² +b²

單位向量符號
U戴帽子∧

都是從勾股定理，商高定理(畢氏定理)來的
Pythagorean theorem

平面上的直角三角形的兩條直角邊的長度平方和等於斜邊長平方
勾長 直邊
股長 底邊
弦長 斜邊

來源：
根據「周髀算經」記載，
商高對周公說 將一根直尺折成一個直角，
兩端連結成一個直角三角形，
如果勾是 3，股是 4， 那麼弦就是 5。

2D distance

√(a²   + b²)
根號(a²+b²)

3D distance

√(x²+y²+z²)
根號(x²+y²+z²)

空間中的兩個點距離
A(ax,ay,az)
B(bx,by,bz)
√((ax-bx)²+(ay-by)²+(az-bz)²)
 根號((ax-bx)²+(ay-by)²+(az-bz)²)

a 是利用兩次勾股定理算出

b 或是利用向量平移，把其中一個點移到原點，
然後另一個點扣掉平移量之後，跟原點計算距離

c 其實就是向量減法的幾何意義

單位向量驗證
把長度/長度
√(x²+y²+z²)/向量長=1/1=1